www.maorpet.com
Reverse Time Migration: The math.
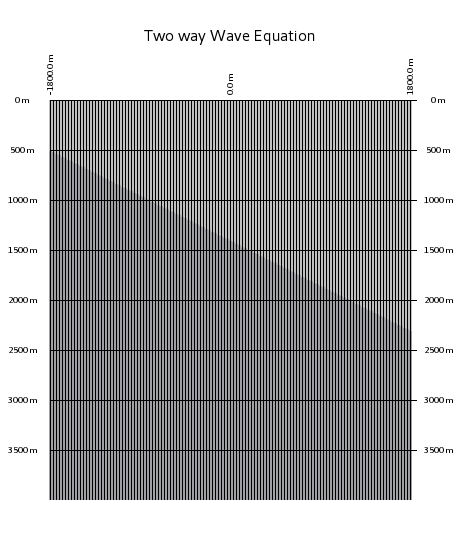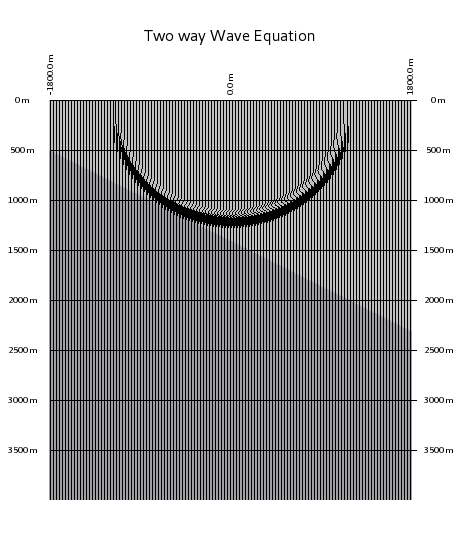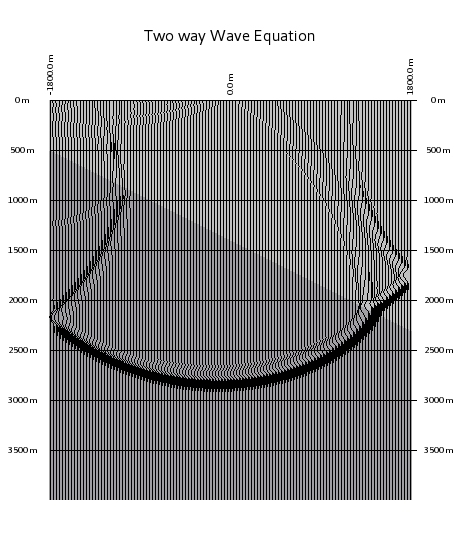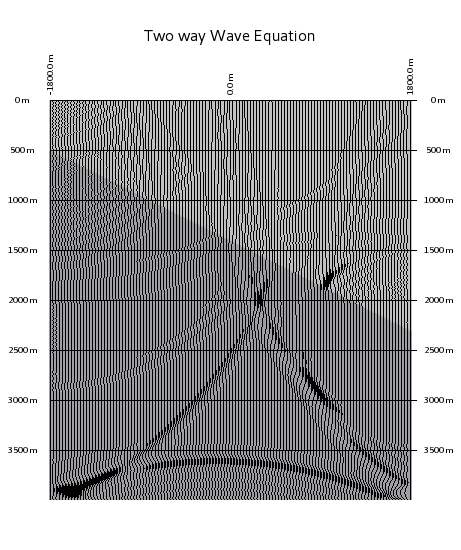
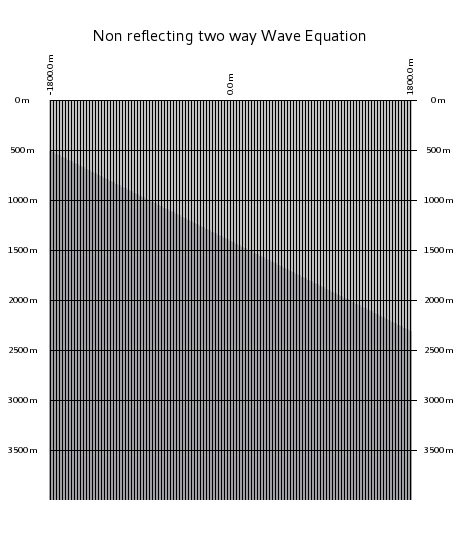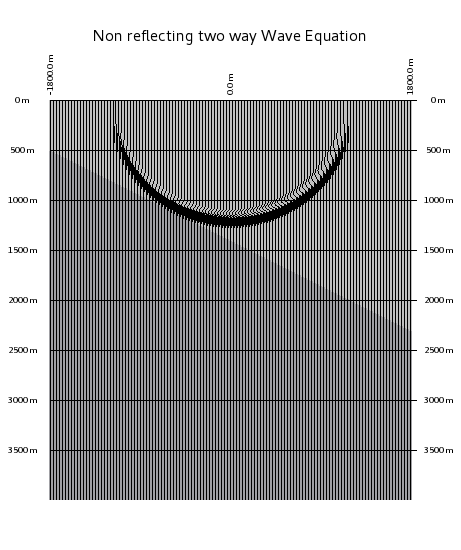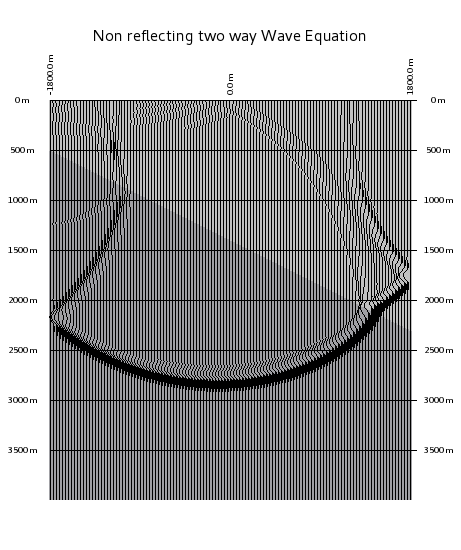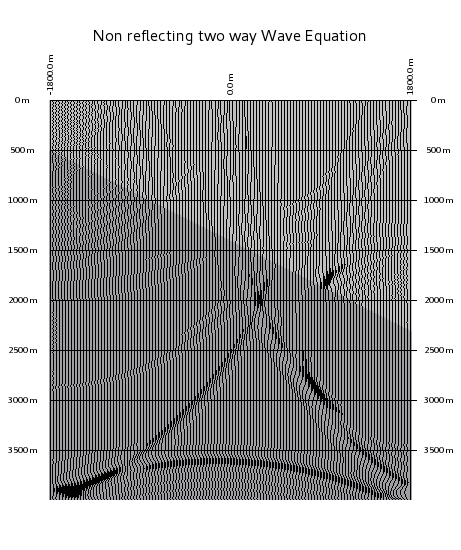
The question is, how can we convince a wave to propagate?
The answer is: use the wave equation. The two pictures above show to solutions. (Not too much difference in between the two ...)
Two way wave equation ?
Yes, we have to use two way wave equation, if we want to handle turning waves as well.
To do it is quite easy: just don't mess up with the square root and associated simplifications.
We will start with our well known Wave Equation. For simplification we stay at 2D, but the 3D version is exactly the same. In case of 2D, we have a slice of the ground to investigate; described by the horizontal and vertical coordinates of x and z. Every (x,z) point of this slice has its wave propagation velocity. We will call this velocity as v(x, z).
The ground slice is covered by a wave field: U(x, z, t). At the beginning this wave field is zero at any (x, z) point, at any time. Now, at a given (xs, zs)point; we introduce some kind of a force. (This might be our time reversed seismic trace, or it might be the source wave.) The result will be; the wave field starts to change, a wave starts to propagate along the ground slice.
The wave field has to satisfy the wave equation.
Here f(xs, zs, t) is the introduced force. Please notice: it is a simple time function at a fixed (x,z) location.
The exercise is: from the known U(x, z, t) we have to compute the U(x, z, t+dt) wave field.
Our only help is: the wave equation.
In the wave equation; there are some second derivatives. We are in the digital, numerical world; we must use numerical solutions. There are no problems with the x and z derivatives; we have plenty of data, we might use any kind of derivative-approximations. In practice they used to use the parabolic approximation: we take one sample before and one sample after the actual sample location, we fit a parabolic curve over the three points; and we take the second derivate of this parabola at the center. In plain words:
Some authors propose more sophisticated second derivative calculations, but the real experience does not show too much benefits. There might be 8th order, Lagrange, ... etc solutions ... as you like.
The question of the time derivate is a little different. We know the U(x, z, t-dt) wave field; at the beginning it is total zero. We also know the U(x, z, t) wave field as well; at the beginning it is also zero, except the location (or locations), where the applied force start to act.
This is still not enough to compute the parabolic second derivate, because the U(x, z, t+dt) is missing. But; instead of going for the second derivate, we use the known elements to compute the missing U(x, z, t+dt).
This is exactly, where the wave equation comes into the picture. We know, the wave field must satisfy the wave equation. Using the wave equation, we have:
We must not forget, that at the right moments we have to add the force values to the proper (x,z) positions too. Out of this formula the unknown U(x, z, t+dt) wave field is easily obtainable.
Please notice: this is the case, when we used the parabolic approximation to compute the second time derivate. To use better approximations of the second time derivate, we must include more points, let's say: t-2dt, t-dt, t, t+dt, t+2dt. This case t+dt and t+2dt are both unknowns. There are some clever solutions (just search the literature on the Internet), but they represent more efforts than benefits.
The wave propagates in he ground.
The ground is represented by the wave propagation velocity field. A very nice point of this type of migration is, that we don't have the limitations of the formerly introduced migrations, we can vary the velocity field horizontally, or vertically, as we like.
Here comes the question of the sampling rate. We can not do too much with the horizontal sampling, the distance between the receiver positions is already fixed, we should use the half of it, if the source position is in between two receiver positions
The vertical sampling rate will be the same, as we want the sampling of the final depth image. There is an interesting stability topic, what is open for scientific discussions. The size of the time steps (as we force the trace samples back into the ground) is related to the spacial sampling rates, to the frequency content and to the shape of the velocity field. Sometimes one has to use very small time steps, to achieve a stable solution. This we will see later on, by taking examples.
But, please notice; these time steps are different (and independent) of the original sampling rate of the seismic trace.
. . .