Sharp edges, no smiles, easy interpretation --- these are some examples of the method, what is called: phase shift migration.

Just for the better understanding; let's go back again to the wave equation, this time to the 3D version.

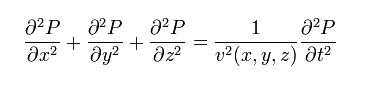
This equation can be anything. Using vector variables it will be elastic, using simple velocity, it will be skalar equation, ... etc.

The following function can be a solution, especially a plane wave, what can go any direction.

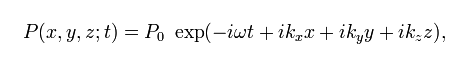
Small exercise: please take a piece of paper and start derivate. It is easy. Place the derivates into the wave equation. After a few simplifications you will see that the condition that our function can be a solution is, that:

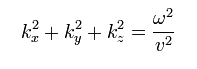
This is nothing else but the dispersion relation. Up to this point we did not say anything special. Things start specialize, when we start working with our formulas. For example in the phase shift method we have to use wave number in z direction. To do this we must take the square root of the dispersion relation. Here we must select either the plus, or the minus part of the square root. This selection will specialize our wave equation; when we use a sign, where the z increases together with the time, we will get a downgoing wave solution; when it is opposite, it will describe and upgoing wave.