www.maorpet.com
Principle of wave field extrapolation (the math)
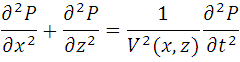
So, here is again our wave equation. The P = P(x,z,t) function is a solution of this beauty. The recorded seismic traces represent only a small slice of this three dimensional solution. Especially they represent a slice at z=0.
We have to talk about the Fourier transform. We will see it more detailed in the "Classic" section, but also you might find unlimited resource on the internet. Here we will use only a small part of the Fourier transform topic.
First of all; the terminology. When we Fourier transform something, we used to say, we put it into frequency domain. The "frequency" as we use it in the everyday talking means time frequency. The sound has a frequency, radio signal has a frequency, ... etc. These are all the counterparts of the time variable. It is measured in Hertz (Hz). For example the A Hz frequency means, that the signal waves A times in a one second time period. The Fourier transform of a time function puts the function into frequency domain. This naming convention has some historical backgrounds.
Beside the time variant; in our case we use some space variants as well. Especially the horizontal x and the vertical z coordinate. We call the Fourier transformed counterparts of these coordinates as space frequencies, or wave numbers. In general they use the kx and kz letters for the wave numbers along the x and z axes, and f, or the Greek omega for the time frequency. There is a small confusion; due to the periodicity a 2*PI multiplier should be included. Usually the f represent the time frequency in Hz, without the multiplier, while omega includes it. You must pay attention to this at the space frequencies, because there is no accepted convention in this regard. Also, in the typing we will use the "w" instead the Greek small omega.
For our purposes we will use a small "rule" of the Fourier transform. This rule says; when the original function is shifted along its axis by an amount, then the Fourier transformed function is multiplied by an exponential, including the shift in the exponent. More precisely:
where ka is the Fourier transformed counterpart of the a variable.
We will use this simple trick to dig down our receivers to the dz depth. First we Fourier transform our shot record both in t and in x. For the time being we can do nothing with the z. As a result, we will have P(kx, z=0, w) Fourier transformed function instead of the original P(x, z=0, t). Now, we can apply the small trick to shift the recorded wave field from 0 to z depth:
The negative sign means that we are digging down. Here we have one problem: we have no idea, what is the kz vertical space frequency (or wave number, if you like). Our only hope to overcome this question is the so called "Dispersion Formula". We will see this formula in details in the "Classic" section, but this moment just believe me: there are millions of solutions to the wave equation. Out of these solutions some describe real waves, but there are others as well. Only those solutions describe real waves, which satisfy the so called "Dispersion Formula", or "Dispersion Relation". This formula gives an obligatory relationship between the frequencies and the wave numbers.
Including this into the previous formula we get:
This is the base of all phase shifting data processing methods. We take our shot record, which is a real physical seismic experiment. We compute the 2 dimensional Fourier transform (in x and t direction). At the same time we create an artificial signal at the actual location of the original source position. It is possible to play with this signal, the outcome will modify the frequency content of the final result. Best to generate this signal analytically, direct in the 2D Fourier domain.
From this point the procedure is: apply the phase shift to both receiver and source wave field, come back to x domain (keep the time domain as it is), multiply the two data set and add together the samples along each x (along each original trace position). This will be the zero shift of the cross correlation.. Place the result on the (x, z, t=0) plain and continue stepping with the z depth variable. You can keep always the original spectra and step direct from zero to the z depth. This case you have to use the average velocities in the Dispersion Formula. Or, you can go by small dz steps, always renewing the original spectra to the new, phase shifted one. This case you must use the interval velocity of the actual dz depth step. The first method is more robust, but there might be discrepancies at the tilted layers. The second one handles all dips correctly but the continuous renewal of the previous spectra increases the computational errors.
...